This game is the 15 Puzzle Game. In this game, there is a 4*4 board with 15 numbers and an empty square. The numbers are then shuffled randomly. The goal of the game is to move the numbers in such a way that the numbers are ordered again as shown in the picture below. The rules are simple. You can only move tiles into the empty tile space.

First of all we need to make a class to represent this board:
class Board:
def __init__(self):
# 4 by 4 board
# self.board is the goal board when first initialized
self.board = [range(1, 5),
range(5, 9),
range(9, 13),
range(13, 16) + ['*']]
# self.goal is later used as a comparison to solve the mixed board
self.goal = []
for i in self.board:
self.goal.append(tuple(i))
self.goal = tuple(self.goal)
# self.empty is the position of empty block
self.empty = [3, 3]Now we need a way to print this graph on the console of Python:
def __repr__(self):
string = ''
for row in self.board:
for num in row:
if len(str(num)) == 1:
string += ' ' + str(num)
elif len(str(num)) > 1:
string += ' ' + str(num)
string += '\n'
return stringWhen you print the board method on the console, it should look like this:
>>> board = Board()
>>> print board
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 *An important thing to remember when you are writing repr is that what you return MUST be a string.
Now, after we have a way to represent our board, we need to be able to do the basic things the player can do. I need to be able to move the empty block up, down, right, and left.
def move_up(self): # move empty block up
try:
if self.empty[0] != 0:
tmp = self.board[self.empty[0]-1][self.empty[1]]
self.board[self.empty[0]-1][self.empty[1]] = '*'
self.board[self.empty[0]][self.empty[1]] = tmp
self.empty = [self.empty[0]-1, self.empty[1]]
except IndexError:
pass
def move_down(self): # move empty block down
try:
tmp = self.board[self.empty[0]+1][self.empty[1]]
self.board[self.empty[0]+1][self.empty[1]] = '*'
self.board[self.empty[0]][self.empty[1]] = tmp
self.empty = [self.empty[0]+1, self.empty[1]]
except IndexError:
pass
def move_right(self): # move empty block right
try:
tmp = self.board[self.empty[0]][self.empty[1]+1]
self.board[self.empty[0]][self.empty[1]+1] = '*'
self.board[self.empty[0]][self.empty[1]] = tmp
self.empty = [self.empty[0], self.empty[1]+1]
except IndexError:
pass
def move_left(self): # move empty block left
try:
if self.empty[1] != 0:
tmp = self.board[self.empty[0]][self.empty[1]-1]
self.board[self.empty[0]][self.empty[1]-1] = '*'
self.board[self.empty[0]][self.empty[1]] = tmp
self.empty = [self.empty[0], self.empty[1]-1]
except IndexError:
passThese 4 methods are the methods in the class that are going to be used to move the empty block. This is when the position of the empty block comes in handy.
We use a try and except to make sure we don't move off the board.
If you have an array and you take the index of [-1], you get the last element of that array. We don't want that to happen and therefore we put an if statement to make sure that the empty block is not at the top of the board.
If it passes these condition, then we can actually move the empty block. We subtract 1 from the row and make that index to be the empty block. We swap the empty block with the previous number that the new empty block has just replaced. We do this for all 4 directions.
After moving the board should look like this:
>>> board = Board()
>>> print board
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 *
>>> board.move_up()
>>> board.move_left()
>>> print board
1 2 3 4
5 6 7 8
9 10 * 11
13 14 15 12We have gotten the basic movements down. Let's make this a real game. In order to do that, we need a way to shuffle the whole board such that there is a game to solve.
def shuffle(self, steps):
for i in range(0, steps):
direction = random.randrange(1, 5)
if direction == 1:
self.move_up()
elif direction == 2:
self.move_right()
elif direction == 3:
self.move_left()
elif direction == 4:
self.move_down()This method will be used to mix the board randomly. I generate a random number between the range 1 to 5 including 1 and excluding 5 which gives me a total of 4 possible numbers. I associate these 4 numbers to each move (up, down, left, right).
Board after shuffled 100 times:
>>> board = Board()
>>> board.shuffle(100)
>>> print board
1 2 4 12
9 5 6 3
10 8 * 7
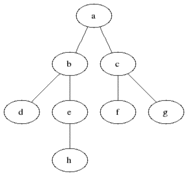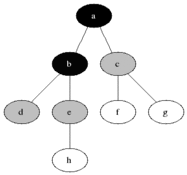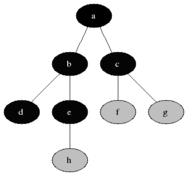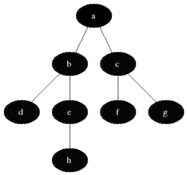
13 14 11 15Now that we have a game to play, here comes the complicated part: to be able to write a function to solve this. The way we're going to solve this is using breadth first search which finds the shortest way to get to the goal. Breadth First Search There are three types of searches : Breadth First Search, Uniform Cost Search, and Depth First Search. In depth first search, you do not care about whether or not there are nodes of different levels. Depth first search always goes deeper down the node tree. Breadth First Search on the other hand explores the node with the most shallow level. As a result, breadth first search reaches the shortest path but depth first search is more efficient on memory. Uniform cost search is for weighted graphs when you go explore the next node that costs the least. For this program, the most applicable search is the Breath First Search since we want to find the shortest path to reach our goal.
Implementation of Breath First Search:
def solve(self):
start = self.convert_to_tuple(self.board)
pred = {}
visited = []
frontier = Queue.Queue()
frontier.put(start)
while frontier.qsize() > 0:
tmp = frontier.get()
if tmp == self.goal:
path = []
while tmp != start:
path.append(pred[tmp][1])
tmp = pred[tmp][0]
return path[::-1]
if tmp not in visited:
visited.append(tmp)
tmpboard = self.match(tmp)
tmpboard.move_up()
if self.convert_to_tuple(tmpboard.board) != tmp:
frontier.put(self.convert_to_tuple(tmpboard.board))
if not pred.has_key(self.convert_to_tuple(tmpboard.board)):
pred[self.convert_to_tuple(tmpboard.board)]=[tmp, 'up']
tmpboard = self.match(tmp)
tmpboard.move_down()
if self.convert_to_tuple(tmpboard.board) != tmp:
frontier.put(self.convert_to_tuple(tmpboard.board))
if not pred.has_key(self.convert_to_tuple(tmpboard.board)):
pred[self.convert_to_tuple(tmpboard.board)]=[tmp, 'down']
tmpboard = self.match(tmp)
tmpboard.move_right()
if self.convert_to_tuple(tmpboard.board) != tmp:
frontier.put(self.convert_to_tuple(tmpboard.board))
if not pred.has_key(self.convert_to_tuple(tmpboard.board)):
pred[self.convert_to_tuple(tmpboard.board)]=[tmp, 'right']
tmpboard = self.match(tmp)
tmpboard.move_left()
if self.convert_to_tuple(tmpboard.board) != tmp:
frontier.put(self.convert_to_tuple(tmpboard.board))
if not pred.has_key(self.convert_to_tuple(tmpboard.board)):
pred[self.convert_to_tuple(tmpboard.board)]=[tmp, 'left']
raise Exception('There is no solution.')In this method called solve, we will output a list of strings that give you directions in order to solve the board ('up', 'down', 'left', 'right'). First thing you have to notice is that you MUST import Queue with the line:
import QueueVisualizing the Problem In this program, each state that the board is in is a node. We are comparing node to node and checking until our current node is the same as the goal board, which means all the numbers are in order. The Variables: start stores the original list used for the board when we initialized this class and is the first node that is explored pred is used in the method at the very end to create the directions to solve the board visited stores all the nodes that we have already checked/visited and explored through frontier is a Queue that stores our plan for which node to explore next. NOTE : Frontier is a Queue which means first in first out Parts The First Part: The first part of this method is the first if statement which checks whether or not our current node is the goal node that we are trying to achieve. If it is, we use our current dictionary and create a list of directions and return that list.
The Second Part:
The second part of this method is the second if statement which adds new nodes to our Queue such that we an explore them. First of all, we have to make sure that we are not visiting the same node twice so we check if our current node is in the visited array. Then there are 4 miniparts for each direction. These miniparts don't vary a lot. From one node of the board I can get to 4 new nodes by moving 4 different directions. I store these 4 possible nodes into the Queue such that I can explore them in the future. Then I add the directions to the dictionary such that, when I do find the solution, I can refer back to the dictionary 'pred' and create a list of directions.
NOTE : Some methods in the solve method are not shown for simplicity. At the bottom of this blog, you will be able to see the whole program with these small methods.
For the complete program, including all methods and implementation details, please visit the GitHub repository.